Применение комплексных чисел для символического метода расчета электрических цепей переменного тока

Символический метод, основанный на использовании комплексных чисел, нашёл широкое применение для расчета сложных цепей переменного тока. Комплексное число состоит из вещественной и мнимой частей . Комплексное число на комплексно-числовой плоскости можно представить вектором. Проекция вектора на вещественную ось (ось абсцисс) соответствует вещественной части комплексного числа . Проекция вектора на мнимую ось (ось ординат) соответствует коэффициенту мнимой единице , - мнимая единица, представляет собой поворотный множитель, умножение на который означает поворот вектора на против часовой стрелки (в электротехнике мнимую единицу обозначают j, чтобы не путать с обозначением тока).

При работе с комплексными числами на плоскости, необходимо помнить, что элементы векторной алгебры и аналитической геометрии на плоскости, также находят широкое применение в теории комплексных чисел.

Как было указано выше, существует три формы записи комплексного числа.

1. Алгебраическая запись

2. Тригонометрическая запись

3. Показательная запись

Для перевода из показательной формы записи комплексного числа в алгебраическую пользуются тригонометрической формой комплексного числа. Для перевода из алгебраической формы записи комплексного числа в показательную определяют модуль и аргумент.

Комплексы тока и напряжения.

Если ток и напряжение изменяются по синусоидальному закону , , то, как указывалось выше, их можно изобразить векторами и, записать комплексными числами:

где и - комплексы тока и напряжения. Точка над комплексами указывает, что ток и напряжение изменяются по синусоидальному закону с определенной частотой ; и - модули комплексов тока и напряжения, они же действующие значения тока и напряжения; и - аргументы комплексов тока и напряжения, они же начальные фазы тока и напряжения .

Комплекс сопротивления.

Для неразветвлённой цепи с и мгновенные значения синусоидального тока и напряжения можно записать так: , и . Тогда комплексы тока и напряжения:

Комплекс полного сопротивления цепи определяется отношением комплекса напряжения к комплексу тока, т.е.

Модулем комплекса полного сопротивления является кажущиеся сопротивление цепи , а аргументом – угол сдвига фаз между током и напряжением .

Алгебраическая форма записи комплекса полного сопротивления

Вещественная часть комплекса полного сопротивления есть активное сопротивление , а коэффициент при мнимой единице - реактивное сопротивление . Знак перед поворотным множителем (мнимой единицей) указывает на характер цепи.

Любую цепь переменного тока можно рассчитывать по законам постоянного тока, если все величины представить в комплексной форме.

Комплекс мощности.

Для неразветвлённой цепи с и мгновенные значения тока и напряжения можно записать в виде:

, и

Комплексы этого напряжения и тока:

и

Комплекс полной мощности цепи определяется произведением комплекса напряжения и сопряженного комплекса тока . У сопряженного комплекса знак перед мнимой единицей меняется на обратный.

Таким образом, модулем комплекса полной мощности является кажущая мощность цепи , а аргументом – угол сдвига фаз между током и напряжением .

Пример:

Для цепи, изображённой на рисунке:

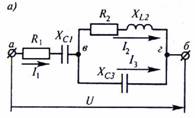
Дано: Ом; Ом; Ом; Ом; Ом; В.

Найти:

1. Токи , и .

2. Напряжения на участках ав и вг.

3. Мощности , и .

4. Угол и характер цепи.

5. Построить векторную диаграмму цепи.

Решение:

1. Комплексы сопротивления участков (по номерам токов) и полного сопротивления цепи:

Комплексное сопротивление участка вг цепи:

Тогда полное сопротивление цепи:

Вектор заданной величины (тока или напряжения) можно направлять в любом направлении.

Однако удобней совмещать эти вектора с вещественной и мнимой частью.

2. В рассматриваемом примере заданное напряжение совместим с вещественной осью, т.е. комплекс общего напряжения:

Комплекс тока цепи , равен комплексу первого тока

Комплексное напряжение на участке ав:

Комплексное напряжение на участке вг:

Комплексы токов и

3, 4. Комплекс полной мощности цепи:

1.Векторная диаграмма изображена на рисунке.

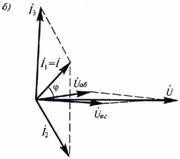
Таким образом, применяя комплексные числа и векторною алгебру на плоскости, можно рассчитывать необходимые электрические схемы переменного тока.