Вариант контрольной работы № 4 с решениями

1. Определить участки выпуклости-вогнутости и точки перегиба функции

Решение

Для нахождения интервалов выпуклости-вогнутости вычислим вторую производную:

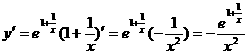
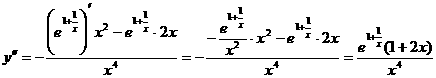
Функция выпуклая вверх, когда 1 + 2х > 0, т. е. при х > -0,5 и выпуклая вниз при х < -0,5. В точке х = - 0,5 функция имеет перегиб.

2. Исследовать функцию и построить график:

Решение

1) Область определения функции

Функция определена во всех точках, кроме х = 0.

2) Точки пересечения графика функции с осями координат

Ось Оу график не пересекает. Найдем точки пересечения с Ох:

х² + 2х – 1 = 0

График функции пересекает ось Оу в точках х₁ и х₂.

3) Интервалы знакопостоянства функции

Решим неравенство:

х² + 2х – 1 > 0

Ветви параболы направлены вверх, значит,

f(x) > 0 при;

f(x) < 0 при .

4) Четность-нечетность функции

Очевидно, данная функция является функцией общего вида.

5) Асимптоты графика функции

В точке х = 0 функция претерпевает разрыв II рода,

, значит, прямая х = 0 является вертикальной асимптотой графика функции.

Прямая у = 1 является горизонтальной асимптотой графика функции, т. к. .

6) Интервалы монотонности функции

Вычислим производную:

Решим неравенство методом интервалов:

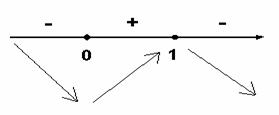
Следовательно, функция убывает при и возрастает при .

7) Экстремумы функции

В точке х = 1 функция имеет максимум, в точке х = 0 у функции разрыв, экстремума нет.

8) Интервалы выпуклости и точки перегиба графика функции

Найдем вторую производную:

Следовательно, при х < 3/2 функция выпуклая вверх,

при х > 3/2 функция выпуклая вниз. При х = 3/2 функция имеет перегиб.

График функции представлен на рисунке:

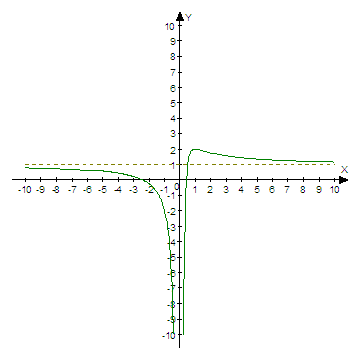
3. Найти частные производные 1-го и 2-го порядков (, , , , ) функции z = 3x²y – x³ – y⁴.

Решение

4. Даны функция z = x² + xy + y², точка A(1, 2) и вектор р = {2, –1}.

Найти:

1) grad z в точке А;

2) производную в точке А по направлению р.

Решение

1) Найдем градиент функции:

grad z = (2x + y, x + 2y).

Вычислим градиент в точке А(1,2):

grad z = (4, 5)

2) Нормируем вектор направления

Затем вычисляем производную по направлению

5. Определить тип особых точек, а также найти наибольшее и наименьшее значения функции

z = x²y +x y + x

в замкнутой области D, ограниченной кривыми:

у = 2, х = 1, х = - 2, у = - 2.

Сделать чертеж области.

Решение

Построим область D:

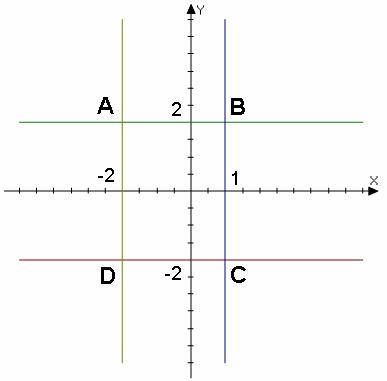
Область представляет собой прямоугольник ABCD.

Найдем стационарные точки функции:

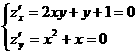
Из последнего уравнения получаем два значения х = 0 и х = -1. Подставляя их в первое уравнение получаем два значения у: y = -1 и y = 1. Значит, стационарными точками функции являются точки (0, -1) и (-1, 1). Обе они принадлежат области. Найдем значения функции в стационарных точках:

z(0, -1) = 0, z(-1, 1) = -1.

Перейдем к поиску максимального и минимального значений функции на границе области . Рассмотрим поочередно участки АВ, ВС, СD и AD.

АВ: y = 2

Функция z(x,y) на этом участке представима в виде функции одной переменной:

z(x,2) = 2x² + 3x

Найдем экстремум этой функции:

точка экстремума х = -3/4. Вычислим значения функции в этой точке, а также на границах: z(-3/4,2) = , z(-2,2) = z (A) =2, z(1,2) = z (B) = 5.

BC: x = 1

z(1,y) = 2y + 1

Экстремумов у функции нет, в точке В значение уже вычислено,

найдем z(C) = z(1,-2) = -3.

CD: y = -2

z(x,-2) = -2х² – х

Экстремум этой функции:

, х = -1/4 – эта точка принадлежит отрезку CD. Вычислим значение в ней и в граничной точке С (в точке С значение функции уже вычислено):

z(-1/4,-2) = 0;

z(D) = z(-2,-2) = -6.

AD: x = -2

z(-2,y) = 2y -2

Экстремумов у этой функции нет, значения в граничных точках А и D уже вычислены.

Теперь определим среди вычисленных значений максимальное и минимальное. Наибольшее значение функции равно ; наименьшее – z(D) = -6.